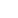Los fractales: un modelo matemática aritmético y geométrico interesante.

Esta semana en la sección del Semanario de Investigaciones IB les compartimos la Monografía en Matemática de nuestro ALUMNI Fernando José Caceros Morales (2018), quien fue asesorado por Luis Horacio Gaytán profesor de dicha asignatura para el Programa del Bachillerato Internacional.

«Los fractales guardan estrecha relación con las sucesiones aritméticas y geométricas infinitas. Estos elementos son definidos como «un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas»¹; en otras palabras es un polígono que se ve afectado del mismo modo de manera innumerable. La Alfombra de Sierpinski² se forma cuando a un cuadrado se le sustrae la novena parte que se sitúa en el centro del cuadrado al separarlo en nueve pedazos iguales, y repitiendo este patrón con los otros ocho cuadros más pequeños restantes, ejemplificado en la ilustración 1. ³

Por ende, al ser la Esponja de Menger⁴ una versión tridimensional5 de la Alfombra de Sierpinski, el proceso por realizar para construir uno es el mismo, pero empleando cubos en lugar de cuadrados, haciendo que, independientemente de cual de las caras del “cubo” se escoja, se verá igual a la Alfombra de Sierpinski con el
mismo numero de iteraciones. Ejemplificándose también en la ilustración 2.

Para leer la investigación completa:

Por medio de esta investigación se pudo llegar a la conclusión de que el emplear fractales como método de filtrado es, en realidad, factible. Esto porque, como se presento en el desarrollo de la monografía, se puede crear un fractal que no ocupe mucho espacio, en cuanto a volumen, y tenga un área superficial muy extensa, como es el caso de la Esponja de Menger que tiene un volumen nulo y un área superficial infinita. Característica que permitiría que el fractal tenga un gran potencial de filtrado.«

La próxima semana estaremos compartiendo otro trabajo de investigación realizado por uno de nuestros ALUMNI y con el apoyo recibido del profesor de la asignatura elegida por él y que forma parte del claustro en el Programa del Bachillerato Internacional de Colegio APDE El Roble.

#SoyInfluencer #SeFuerteSeRoble #RezoPorElFinDeLaPandemia

^{1 (Fractal, 2018)
2 (Waclaw Sierpinski, 1916)
3 (Sierpiński gasket, 2012)
4 (Karl Menger, 1926)}