Esta semana en la sección del Semanario de Investigaciones IB les compartimos la monografía en Matemática de nuestro ALUMNI Juan David Alfaro González (2018), quien fue asesorado por el profesor Luis Horacio Gaytán, profesor de dicha asignatura para el Programa del Bachillerato Internacional.

Introducción

«El tablero o máquina de Galton es uno de los inventos matemáticos con características especiales. Sin parecerlo, reúne muchos conceptos matemáticos importantes, como la geometría, calculo, probabilidad, etc. Consiste en un tablero de n filas, diseñado simétricamente divididos por clavos. La primera fila tiene 1 clavo en el centro, la fila 2 con 2 clavos separados a la misma distancia del clavo de arriba solo que uno a la izquierda y el otro a la derecha. Se sigue el mismo patrón hasta alcanzar el número de filas deseado.

Este invento fue utilizado en un inicio por Galton para descubrir el teorema del límite central. Pero hoy en día se encuentra en juegos de ferias, debido a su comportamiento. Cuando se lanzan cincos o canicas desde el punto más alto, las canicas se distribuyen en forma de Campana de Gauss. Si el tablero está diseñado de forma simétrica, es decir todos los clavos mantienen la misma distancia, y si todos los caminos tienen el mismo ancho y longitud, la distribución es la misma sin importar el mismo número de filas. Por eso surge el interés, que características matemáticas contiene el tablero para que esto ocurra de esta manera. Que conceptos matemáticos están detrás de tablero.

El propósito de este trabajo de investigación será indagar cómo se comporta el tablero de Galton. Primero se analizará la teoría. Se estudiará le parte de geometría y simetría del tablero, y que características contiene. Luego la probabilidad que tiene la canica de llegar a determinado camino dependiendo del número de filas que contenga. Estudiando todas las rutas posibles a determinado punto. Encontrando la formula general de dos maneras distintas. La primera por combinatoria partiendo de un análisis del triángulo de pascal, y por último con el concepto de la distribución normal.

                Luego se graficará la función de probabilidad del tablero teórico, utilizando las fórmulas encontradas, para comprobar si se tiene la forma de campana de Gauss esperada. Esto se contrastará con una función experimental. Para ello, se diseñó un tablero de Galton experimental. Se realizaron pruebas con 1,000 intentos, y se graficaron los datos en una función de probabilidad con respecto a los caminos.

                Por último, por medio de una prueba de hipótesis se contrastaran ambos casos, para comprobar si mantienen relación, y analizar cuáles son los principales aspectos que debe de tener un tablero experimental para que se comporte lo más parecido al análisis teórico.

Para leer la investigación completa:

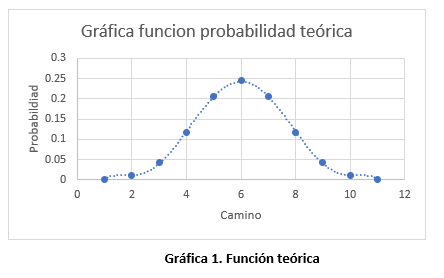
Podemos apreciar que la función tiene la forma de la Campana de Gauss. Definida como «representación gráfica de la distribución normal de un grupo de datos. Éstos se reparten en valores bajos, medios y altos, creando un gráfico de forma acampanada y simétrica con respecto a un determinado parámetro» Es curioso como un tablero de Galton se comporta de la misma manera que un concepto matemático que es utilizado para cálculos astronómicos y estadísticos de poblaciones. La ecuación de la campana de Gauss está dada, por concepto, como:

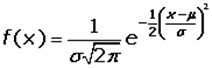
Este resultado era el que esperábamos cuando se calculó la fórmula 4 con la distribución normal, ya que esta se comporta como una campana de Gauss, la cual posee ciertas características importantes:^[1]

• Es una distribución simétrica.

• Es asintótica, es decir sus extremos nunca tocan el eje horizontal, cuyos valores tienden a infinito.

• En el centro de la curva se encuentran la media, la mediana y la moda.

• El área total bajo la curva representa el 100% de los casos.

• Los elementos centrales del modelo son la media y la varianza.«

^{[1] http://www.medwave.cl/link.cgi/medwave/series/mbe04/5033?ver=sindiseno Ultima visita (05/10/2018)}

La próxima semana estaremos compartiendo otro trabajo de investigación realizado por uno de nuestros ALUMNI y con el apoyo recibido del profesor de la asignatura elegida por él y que forma parte del claustro en el Programa del Bachillerato Internacional de Colegio APDE El Roble.

#SoyInfluencer #SeFuerteSeRoble #RezoPorElFinDeLaPandemia